Unidad 5: Introducción a la animación por computadora

Introducción a la animación por computadora

5.1 Historia, evolución y aplicación de la graficación por computadora.

1919-1990

Creación de la Primera Computadora ENIAC por Jhon Presper Mauchly y John William Mauchly.

ENIAC (Electronic Numerical Integrator And Computer) utilizado por el Laboratorio de Investigación Balística del Ejercito de los Estados Unidos.

Era totalmente digital ejecutaba sus procesos y operaciones mediante instrucciones en lenguaje máquina, a diferencia de las otras máquinas computadoras contemporáneas de procesos analógicos.

Presentada en público el 15 de febrero de 1946.

Ocupaba una superficie de 167 m² y operaba con un total de 17.468 válvulas electrónicas o tubos de vacío que a su vez permitían realizar cerca de 5000 sumas y 300 multiplicaciones por segundo.

1950.

Computadoras Digitales.

Están basadas en dispositivos biestables que solo pueden tomar uno o dos valores posibles tienen como ventaja el poder ejecutar diferentes programas para diferentes problemas sin tener la necesidad de modificar físicamente la computadora.

La graficación tuvo sus inicios con el surgimiento de las computadoras digitales.

1950-1960

Inicia la graficación en 2D.

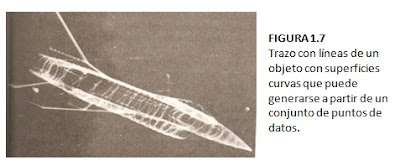
El primer avance de la computación gráfica fue la utilización de los rayos catódicos. La gráfica de vector almacena datos  geométricos precisos, topología y estilo como posiciones de coordenadas de puntos, las uniones entre puntos y el color, el grosor y posible relleno de las formas.

La mayor parte de los sistemas de vectores gráficos también puede  usar primitivas geométricas de forma estándar como círculos y rectángulos.

1956-1959

Refresh TUbe

Divide la pantalla en millones de pixeles iluminado o no en cada barrido de la imagen.

1976

Se forma Siggraph

ACM asociación de máquinas computadoras forma un grupo de interés especial en aplicaciones gráficas.

1980

Auge de Graficación.

·         Se dan grandes avances en el hardware permitiendo mejor desarrollo de la graficación.

·         Graficación en la T.V y uso personal.

·         Avalancha de comercialización de programas CAD, más abiertos y sofisticados a precios accesibles.

·         Turner Whitted publicó un artículo en el año 80 sobre un nuevo método de representación para simular superficies altamente reflexivas. Conocido hoy como raytracing.1999 – 2000.

 

En la actualidad

La mayoría de las personas que trabajan con gráficos utilizan computadoras de grandes capacidades: discos duros de terabytes, tarjetas gráficas aceleradoras de video con memoria en gigabytes, mouse óptico y memoria RAM en el orden de los gigas. También son muy utilizadas las computadoras Macintosh especialmente en lo relacionado a efectos especiales y gráficos de animación.

5.2 Tipos de animación 2D

Animación 2D: En este tipo de animación sólo pueden moverse horizontalmente (movimientos hacia adelante y hacia atrás) y verticalmente (movimientos hacia arriba y hacia abajo). Los objetos son planos, como en una fotografía.

Tipos

5.2.1 Tweening

Es un término usado específicamente para las técnicas tradicionales de animación.

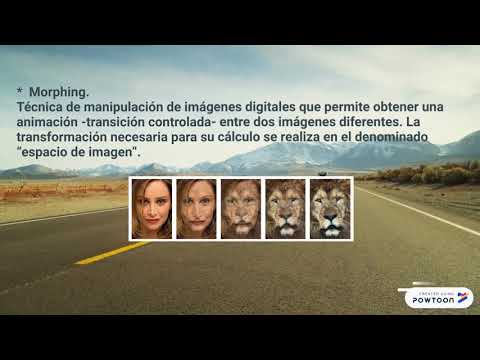
5.2.2 Morphing

En el morphing de imágenes se utilizan dos efectos básicos; la deformación de la imagen, redistribuyendo sus colores y formas, y el fundido de dos imágenes, pasando de forma continúa de una a otra. Ambos efectos parten de una descomposición del espacio de la imagen en una malla de triángulos. Para especificar un cambio continuo en la forma de la imagen basta con describir cómo varía la posición de los vértices de la malla de un instante de tiempo al instante posterior.

El morphing se produce automáticamente cuando se mueven los vértices sin alterar las coordenadas de textura originales.

5.2.3 Onion skinning

es una técnica de gráficación  2D utilizada en la creación de dibujos animados y películas de edición para ver varias imágenes a la vez. De esta manera, el animador o editor puede tomar decisiones sobre cómo crear o cambiar una imagen basada en la imagen anterior en la secuencia.

5.3 Tipos de animación 3D

Animación 3D: En este caso, los objetos también pueden moverse más cerca o más lejos de la persona que ve la animación. Tiene un nivel de calidad y detalle que lo vuelve muy cercano a las imágenes de la realidad, en algunos casos haciéndose imperceptible la diferencia entre la animación y un objeto real.

5.3.1 Cel-Shaded

Es un tipo de renderización no fotorrealista diseñada para hacer que los gráficos por computadora parezcan dibujados a mano. Las sombras planas se usan comúnmente para imitar el estilo de los cómics o dibujos animados.

5.3.2 Morph

En este caso no se trata de modificar una imagen sino la forma del objeto en tres dimensiones. Este cambio continuo puede utilizarse en animación para representar deformaciones o crear efectos visuales. Otro uso, más técnico, consiste en suavizar las transiciones entre diferentes representaciones de un mismo objeto cuando éstas tienen diferente nivel de detalle.

5.3.3 Skeletal

Se crea una representación simplificada del cuerpo del personaje, análogo a un esqueleto o a un stickman.  En personajes humanos y animales, muchas partes del modelo de esqueleto corresponden a la ubicación real de los huesos, pero la animación del modelo de esqueleto skeletal animation es también utilizada para animar otras cosas, como expresiones faciales.

5.3.4 Motion Capture

La captura de movimiento (del inglés motion capture, o motion tracking, también abreviada mocap) es una técnica de grabación de movimiento, en general de actores y de animales vivos, y el traslado de dicho movimiento a un modelo digital, realizado en imágenes de computadora.

Casa 3D

Sweet Home 3D

Es un editor CAD de ingeniería, arquitectura y construcción bajo licencia GNU General Public License para el diseño de los muebles de una vivienda en un plano 2D, y una vista previa en 3D

box

prueba

Unidad 4

Relleno de polígonos

En geometría, un polígono es una figura plana compuesta por una secuencia finita de segmentos rectos consecutivos que cierran una región en el plano. Estos segmentos son llamados lados, y los puntos en que se intersecan se llaman vértices.

En un sentido amplio, se define como una región del espacio delimitada por un conjunto de líneas (aristas) y cuyo interior puede estar rellenado por un color o patrón dado.

La tarea de rellenar a figuras primitivas puede ser dividida en dos partes: la decisión de cuáles pixeles se tienen que rellenar (que depende de la forma de la primitiva modificada por el recortado), y la decisión más sencilla de cuál valor rellenarlos.

MÉTODO DE RELLENO DE POLÍGONOS CON  COLOR

SCAN-LINE

 Fila a fila van trazando lineas de color entre aristas.                                                              para scan-line que cruce el polígono se busca en la intersección entre las lineas de barrido y las aristas del polígono.

• Dichas intersecciones se ordenan y se rellenan a pares.

LINEA DE BARRIDO

     Es valido para polígonos cóncavos como convexos. Incluso para si el objeto tiene huecos interiores.

     Funcionan en el trozo de lineas horizontales, denominadas lineas de barridos, que intersectan un numero de veces, permitiendo a partir de ella identificar los puntos que se consideran interiores al polígono.

INUNDACIÓN

• Empieza en un interior y pinta hasta encontrar la frontera del objeto.
• Partimos de un punto inicial (x,y), un colo de relleno y  un color de frontera.
•  El algoritmo va testeando los píxeles vecinos a los ya pintados, viendo si son frontera o no.
• No solo sirven para polígonos, sino para cualquier área curva para cualquier imagen AE se usan los programas de dibujo.

FUERZA BRUTA

• Calcula una caja contenedora del objeto.
• Hace un barrido interno de la caja para comprobar c/pixel este dentro del polígono.
• Con polígonos simétricos basta con que hagamos un solo barrido en una sección y replicar los demás pixeles.
• Requiere aritmética punto-flotante, esto lo hace preciso y costoso.

ALTERNATIVAS PARA LA SITUACIÓN INICIAL DEL PATRÓN

Consiste en situar el punto asociado a la esquina superior izquierda del patrón en un vértice del polígono.

1. Considerar la región a rellenar en toda la pantalla y por lo tanto el patrón se citua en el origen de esta (esquina superior izquierda).
   

EJEMPLO DE SCAN-LINE

• Encontrar las intersecciones de los scanlines en el polígono.
• Almacenar las intersecciones en alguna estructura de datos ET (edge table), de manera ordena ascendiente en Y y en X  en  buckets.
• Rellenar los spans usando la estructura.
• Usar algún criterio de paridad para saber cuando un intervalo debe ser rellenado o no.

Proyecto Factal

Un fractal es un objeto geométrico cuya estructura básica, fragmentada o aparentemente irregular, se repite a diferentes escalas.1​ El término fue propuesto por el matemático Benoît Mandelbrot en 1975 y deriva del latín fractus, que significa quebrado o fracturado. Muchas estructuras naturales son de tipo fractal. La propiedad matemática clave de un objeto genuinamente fractal es que su dimensión métrica fractal es un número racional no entero.

Si bien el término "fractal" es reciente, los objetos hoy denominados fractales eran bien conocidos en matemáticas desde principios del siglo XX. Las maneras más comunes de determinar lo que hoy denominamos dimensión fractal fueron establecidas a principios del siglo XX en el ámbito de la teoría de la medida..

Figura 3D

Formas Geométricas Tridimensionales (Superficies planas y Curvas)

En este caso trataremos con las proyecciones que van del espacio al plano (3D a 2D). La proyección de objetos tridimensionales serán definidos por la intersección de líneas rectas que van desde un centro de proyección u ojo, hasta cada punto del objeto.
Proyección Acotada

Es una proyección ortogonal sobre la que se acotan en cada punto, línea, u objeto representado la altura (cota) del mismo con respecto a cualquier plano de referencia que sea paralelo al plano de proyección. La proyección acotada es muy práctica cuando es necesario representar gráficamente objetos irregulares; razón por la cual se usa frecuentemente para el diseño de techos de viviendas; construcción de puentes, represas, acueductos, gasoductos, carreteras, determinación de áreas de parcelas, trazado de linderos, y dibujos topográficos de plantas y perfiles de terrenos, entre otros.


Proyección Cónica.

Denominada también perspectiva. Se obtiene cuando el punto de observación y el objeto se encuentran relativamente cercanos. Es el sistema de representación gráfico en donde el haz de rayos proyectantes confluye en un punto (el ojo del observador), proyectándose la imagen en un plano auxiliar situado entre el objeto a representar y el punto de vista.


PROYECCIÓN ORTOGONAL

La Proyección ortogonal es aquella cuyas rectas proyectantes auxiliares son perpendiculares al plano de proyección (o a la recta de proyección), estableciéndose una relación entre todos los puntos del elemento proyectante con los proyectados.

Existen diferentes tipos:
Vista A: Vista frontal o alzado
Vista B: Vista superior o planta
Vista C: Vista derecha o lateral derecha
Vista D: Vista izquierda o lateral izquierda
Vista E: Vista inferior
Vista F: Vista posterior


PROYECCIÓN OBLICUA.

Es aquella cuyas rectas proyectantes auxiliares son oblicuas al plano de proyección, estableciéndose una relación entre todos los puntos del elemento proyectante con los proyectados.

Una proyección Oblicua se obtiene proyectando puntos a lo largo de líneas paralelas que no son perpendiculares al plano de proyección. La figura muestra una proyección oblicua de un punto (x, y, z) por una línea de proyección a la posición (xp, Yp).









ECUACIONES DE PLANO
Los parámetros que especifican la orientación especial de cada polígono se obtienen de los valores coordenados de los vértices y las ecuaciones que definen los planos poligonales. Estos parámetros de planos se utilizan en transformaciones de visión, modelos de sombreado y algoritmos de superficies ocultas que determinan que líneas y planos se traslapan a lo largo de la línea de visión.
La ecuación de una superficie plana puede expresarse así: Ax + By + Cz + D = 0
Donde (x,y,z) es cualquier punto de plano. Los coeficientes A, B, C, D son constantes que pueden calcularse utilizando los valores coordenados de tres puntos no coloniales en el plano. Comúnmente, se usan las coordenadas de tres vértices sucesivos en una frontera de un polígono para hallar valores de estos coeficientes. Al denotar las coordenadas de tres vértices de un polígono como (x1, y1, z1), (x2, y2, z2) y (x3, y3, z3), se puede resolver el siguiente conjunto de ecuaciones planas simultáneas para las razones A/D, B/D y C/D:

(A / D)xi + (B / D)yi + (C / D)zi = -1 i = 1, 2, 3

Utilizando un método de solución como la regla de Cramer, se puede escribir la solución de los parámetros del plano en forma de determinantes:




Podemos ampliar los determinantes y escribir los cálculos de los coeficientes del plano en la forma explícita:

A = y1(z2 − z3 ) + y2 (z3 − z1) + y3(z1 − z2 )

B = z1(x2 − x3 ) + z2 (x3 − x1) + z3(x1 − x2 )

C = x1(y2 − y3 ) + x2 (y3 − y1) + x3(y1 − y2 )

D = −x1(y2z3 − y3z2 ) − x2 (y3z1 − y1z3 ) − x3(y1z2 − y2z1)


Los valores de A, B, C y D se almacenan en la estructura de datos que contiene la información de coordenadas y atributos referente al polígono definido en este plano.

La orientación de una superficie plana se especifica por medio del vector normal al plano, como se muestra en la figura 1.4.Este vector normal tridimensional tiene las coordenadas cartesianas (A, B, C).








Puesto que con frecuencia trabajamos con superficies poligonales que encierran un objeto interior, se necesita distinguir entre los lados de la superficie.

El lado del plano que da la cara al objeto interior se denomina “interior” y el lado visible o externo se llama “exterior”. Si se especifican vértices en un sentido igual al del reloj cuando se observa el lado externo del plano en su sistema coordenado por la derecha, la dirección del vector normal ira de adentro hacia afuera. Esto se demuestra para un plano de un cubo unitario de la figura 1.5.

Para determinar los componentes del vector normal de la superficie sombreada que se muestra en la figura 1.5, se seleccionan tres de los cuatros vértices situados a lo largo de la frontera del polígono.








Estos puntos se seleccionan en un sentido igual al del reloj cuando observamos el exterior del cubo hacia el origen.

Las coordenadas de estos vértices, en el orden seleccionado, se utilizan en la ecuacion de la figura 1.4 a fin de obtener los coeficientes del plano:

A = 1, B = 0, C = 0, D = -1. El vector normal de este plano esta en el sentido del eje x positivo.Las ecuaciones del plano se utiliza también para identificar puntos interiores y exteriores. Cualquier punto (x, y, z) exterior aun plano satisface la desigualdad.

Ax + By + Cz + D > 0

Análogamente, cualquier punto situado en el interior del plano produce un valor negativo de la expresión Ax + By + Cz + D. Para la superficie sombreada de la figura 1.5, cualquier punto exterior al plano cumple la desigualdad x - 1 < 0, mientras que cualquier punto interior al plano tiene un valor de coordenadas x menor que 1.


SUPERFICIES CURVAS

Los despliegues tridimensionales de las superficies curvas pueden generarse a partir de un conjunto de entrada de las funciones matemáticas que define las superficies o bien a partir de un conjunto de puntos de datos especificados por el usuario. Cuando se especifican funciones de curvas, un paquete puede emplear las ecuaciones definidoras para localizar y graficar posiciones de pixeles a lo largo de la trayectoria de la curva, casi igual como sucede con las curvas en dos dimensiones. Un ejemplo de la clase de superficies que pueden generarse a partir de una definición funcional se da en la figura 1.6. A partir de un conjunto de datos de entrada, un paquete determina las descripciones funcionales de la curva que mejor se ajusta a los puntos de datos según las restricciones de la aplicación. En la figura 1.7 se muestra un objeto cuyas superficies curvas pueden ser definidas por un conjunto de entrada de punto de datos.






Podemos representar una línea curva tridimensional en forma analítica con la pareja de funciones.

y=f(x), z=g(x)
Con la coordenada x seleccionada como variable independiente. Los valores de las variables dependientes y, z se determinan después a partir de las ecuaciones 1.6 a medida que se avanza a través de valores de x de un extremo de la línea al otro. Esta representación tiene algunas desventajas. Si se desea una grafica alisada, se debe cambiar la variable independiente siempre que la primera derivada (pendiente) de f(x) o bien g(x) se vuelve mayor que 1. Esto significa que se debe verificar continuamente los valores de las derivadas, que pueden volverse infinitas en algunos puntos. Asimismo, las ecuaciones anteriores ofrecen un formato desproporcionado para representar funciones con valores múltiples. Una representación más propicia de las curvas para aplicaciones de las graficas es en términos de ecuaciones paramétricas.

Formas Geométricas