En este caso trataremos con las proyecciones que van del espacio al plano (3D a 2D). La proyección de objetos tridimensionales serán definidos por la intersección de líneas rectas que van desde un centro de proyección u ojo, hasta cada punto del objeto.
Proyección Acotada
Es una proyección ortogonal sobre la que se acotan en cada punto, línea, u objeto representado la altura (cota) del mismo con respecto a cualquier plano de referencia que sea paralelo al plano de proyección. La proyección acotada es muy práctica cuando es necesario representar gráficamente objetos irregulares; razón por la cual se usa frecuentemente para el diseño de techos de viviendas; construcción de puentes, represas, acueductos, gasoductos, carreteras, determinación de áreas de parcelas, trazado de linderos, y dibujos topográficos de plantas y perfiles de terrenos, entre otros.
Proyección Cónica.
Denominada también perspectiva. Se obtiene cuando el punto de observación y el objeto se encuentran relativamente cercanos. Es el sistema de representación gráfico en donde el haz de rayos proyectantes confluye en un punto (el ojo del observador), proyectándose la imagen en un plano auxiliar situado entre el objeto a representar y el punto de vista.

PROYECCIÓN ORTOGONAL
La Proyección ortogonal es aquella cuyas rectas proyectantes auxiliares son perpendiculares al plano de proyección (o a la recta de proyección), estableciéndose una relación entre todos los puntos del elemento proyectante con los proyectados.
Existen diferentes tipos:
Vista A: Vista frontal o alzado
Vista B: Vista superior o planta
Vista C: Vista derecha o lateral derecha
Vista D: Vista izquierda o lateral izquierda
Vista E: Vista inferior
Vista F: Vista posterior

PROYECCIÓN OBLICUA.
Es aquella cuyas rectas proyectantes auxiliares son oblicuas al plano de proyección, estableciéndose una relación entre todos los puntos del elemento proyectante con los proyectados.
Una proyección Oblicua se obtiene proyectando puntos a lo largo de líneas paralelas que no son perpendiculares al plano de proyección. La figura muestra una proyección oblicua de un punto (x, y, z) por una línea de proyección a la posición (xp, Yp).

ECUACIONES DE PLANO
Los parámetros que especifican la orientación especial de cada polígono se obtienen de los valores coordenados de los vértices y las ecuaciones que definen los planos poligonales. Estos parámetros de planos se utilizan en transformaciones de visión, modelos de sombreado y algoritmos de superficies ocultas que determinan que líneas y planos se traslapan a lo largo de la línea de visión.
La ecuación de una superficie plana puede expresarse así: Ax + By + Cz + D = 0
Donde (x,y,z) es cualquier punto de plano. Los coeficientes A, B, C, D son constantes que pueden calcularse utilizando los valores coordenados de tres puntos no coloniales en el plano. Comúnmente, se usan las coordenadas de tres vértices sucesivos en una frontera de un polígono para hallar valores de estos coeficientes. Al denotar las coordenadas de tres vértices de un polígono como (x1, y1, z1), (x2, y2, z2) y (x3, y3, z3), se puede resolver el siguiente conjunto de ecuaciones planas simultáneas para las razones A/D, B/D y C/D:
(A / D)xi + (B / D)yi + (C / D)zi = -1 i = 1, 2, 3
Utilizando un método de solución como la regla de Cramer, se puede escribir la solución de los parámetros del plano en forma de determinantes:
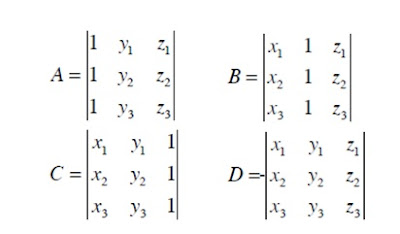
Podemos ampliar los determinantes y escribir los cálculos de los coeficientes del plano en la forma explícita:
A = y1(z2 − z3 ) + y2 (z3 − z1) + y3(z1 − z2 )
B = z1(x2 − x3 ) + z2 (x3 − x1) + z3(x1 − x2 )
C = x1(y2 − y3 ) + x2 (y3 − y1) + x3(y1 − y2 )
D = −x1(y2z3 − y3z2 ) − x2 (y3z1 − y1z3 ) − x3(y1z2 − y2z1)
Los valores de A, B, C y D se almacenan en la estructura de datos que contiene la información de coordenadas y atributos referente al polígono definido en este plano.
La orientación de una superficie plana se especifica por medio del vector normal al plano, como se muestra en la figura 1.4.Este vector normal tridimensional tiene las coordenadas cartesianas (A, B, C).
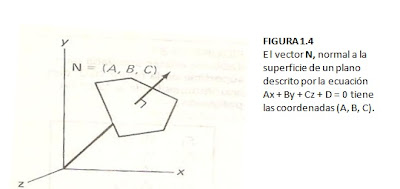
Puesto que con frecuencia trabajamos con superficies poligonales que encierran un objeto interior, se necesita distinguir entre los lados de la superficie.
El lado del plano que da la cara al objeto interior se denomina “interior” y el lado visible o externo se llama “exterior”. Si se especifican vértices en un sentido igual al del reloj cuando se observa el lado externo del plano en su sistema coordenado por la derecha, la dirección del vector normal ira de adentro hacia afuera. Esto se demuestra para un plano de un cubo unitario de la figura 1.5.
Para determinar los componentes del vector normal de la superficie sombreada que se muestra en la figura 1.5, se seleccionan tres de los cuatros vértices situados a lo largo de la frontera del polígono.
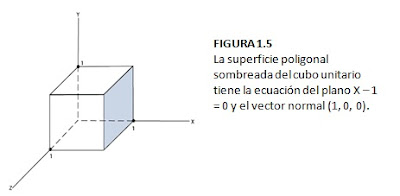
Estos puntos se seleccionan en un sentido igual al del reloj cuando observamos el exterior del cubo hacia el origen.
Las coordenadas de estos vértices, en el orden seleccionado, se utilizan en la ecuacion de la figura 1.4 a fin de obtener los coeficientes del plano:
A = 1, B = 0, C = 0, D = -1. El vector normal de este plano esta en el sentido del eje x positivo.Las ecuaciones del plano se utiliza también para identificar puntos interiores y exteriores. Cualquier punto (x, y, z) exterior aun plano satisface la desigualdad.
Ax + By + Cz + D > 0
Análogamente, cualquier punto situado en el interior del plano produce un valor negativo de la expresión Ax + By + Cz + D. Para la superficie sombreada de la figura 1.5, cualquier punto exterior al plano cumple la desigualdad x - 1 < 0, mientras que cualquier punto interior al plano tiene un valor de coordenadas x menor que 1.
SUPERFICIES CURVAS
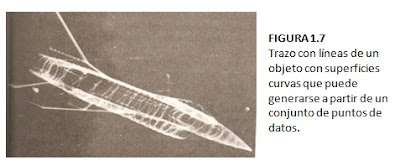
Los despliegues tridimensionales de las superficies curvas pueden generarse a partir de un conjunto de entrada de las funciones matemáticas que define las superficies o bien a partir de un conjunto de puntos de datos especificados por el usuario. Cuando se especifican funciones de curvas, un paquete puede emplear las ecuaciones definidoras para localizar y graficar posiciones de pixeles a lo largo de la trayectoria de la curva, casi igual como sucede con las curvas en dos dimensiones. Un ejemplo de la clase de superficies que pueden generarse a partir de una definición funcional se da en la figura 1.6. A partir de un conjunto de datos de entrada, un paquete determina las descripciones funcionales de la curva que mejor se ajusta a los puntos de datos según las restricciones de la aplicación. En la figura 1.7 se muestra un objeto cuyas superficies curvas pueden ser definidas por un conjunto de entrada de punto de datos.
Podemos representar una línea curva tridimensional en forma analítica con la pareja de funciones.
y=f(x), z=g(x)
Con la coordenada x seleccionada como variable independiente. Los valores de las variables dependientes y, z se determinan después a partir de las ecuaciones 1.6 a medida que se avanza a través de valores de x de un extremo de la línea al otro. Esta representación tiene algunas desventajas. Si se desea una grafica alisada, se debe cambiar la variable independiente siempre que la primera derivada (pendiente) de f(x) o bien g(x) se vuelve mayor que 1. Esto significa que se debe verificar continuamente los valores de las derivadas, que pueden volverse infinitas en algunos puntos. Asimismo, las ecuaciones anteriores ofrecen un formato desproporcionado para representar funciones con valores múltiples. Una representación más propicia de las curvas para aplicaciones de las graficas es en términos de ecuaciones paramétricas.
Formas Geométricas

No hay comentarios.:
Publicar un comentario