Teoría de la Parábola

Parábola

En matemática, la parábola(del griego παραβολή) es la sección cónica resultante de cortar un cono recto con un plano paralelo a su generatriz: [] (es una línea que a causa de su movimiento conforma una figura geométrica, que a su vez depende de la directriz. La generatriz puede ser una línea recta o curva) []


Definición: Se define también como el lugar geométrico de los puntos de un plano que equidistan de una recta llamada directriz, y un punto exterior a ella llamado foco.

La parábola presenta en llega varios elementos que la componen como son:

• Directriz:

En geometría la directriz es aquella línea, superficie o volumen que determina las condiciones de generación de otra línea, superficie o volumen (que se llama generatriz)

• FOCO:

El foco de una curva o de una superficie es un punto singular, por lo general no perteneciente a ella, respecto del cual se mantienen constantes determinadas distancias relacionadas con todos los puntos de la misma. Una figura puede tener asociados más de un foco.



 El foco de la parábola es un punto. Respecto del foco, cada punto de la parábola posee la misma distancia que hasta una recta llamada directriz.

• Lado recto:

Al segmento de recta comprendido por la parábola, que pasa por el foco y es paralelo a la directriz, se le conoce como lado recto. La longitud del lado recto es siempre 4 veces la distancia focal.

• Vértice

Es el punto de intersección de la parábola

• Eje

Es la recta perpendicular a la directriz que paso por el foco.

• Distancia focal

La distancia focal o longitud focal de una lente es la distancia entre el centro óptico de la lente o plano nodal posterior y el foco (o punto focal) cuando enfocamos al infinito.

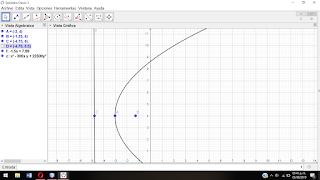
A continuación mostraremos los ejercicios expuestos en clase y resueltos también en geogebra:

Ejercicio 1;

 Ejercicio 2;

Ejercicio 3 ;

Revisa este video 

ejercicio 4 y 5

                                                                y^2-7x-8y-5=0

                                                              y^2-15x+16y+79=0

Linea Recta

Ecuación de la recta


Para entrar en esta materia y para entender lo que significa la Ecuación de la Recta es imprescindible estudiar, o al menos revisar, lo referido a Geometría analítica y Plano cartesiano .


La idea de línea recta es uno de los conceptos intuitivos de la Geometría (como son también el punto y el plano ).


La recta se puede entender como un conjunto infinito de puntos alineados en una única dirección. Vista en un plano, una recta puede ser horizontal, vertical o diagonal (inclinada a la izquierda o a la derecha).






Ecuación general de la recta


Esta es una de las formas de representar la ecuación de la recta.


De acuerdo a uno de los postulados de la Geometría Euclidiana, para determinar una línea recta sólo es necesario conocer dos puntos (A y B) de un plano (en un plano cartesiano) , con abscisas (x) y ordenadas (y) .



Recuerden que es imprescindible dominar todos los aspectos sobre el Plano cartesiano pues la Ecuación de la recta no tiene existencia conceptual sin un Plano cartesiano.



Ahora bien, conocidos esos dos puntos, todas las rectas del plano, sin excepción, quedan incluidas en la ecuación
Ax + By + C = 0


Que también puede escribirse como



ax + by + c = 0

Ecuacion 1

Ecuacion 2

DEFINICIÓN DE GRAFICACION

Graphics: are visual images or designs on some surface,such as a wall, canvas,screen paper or stone to inform,ilustrate.

La graficación es el arte o la ciencia de producir imágenes gráficas con la ayuda de la computadora.

La graficacion por computadora es una de las áreas más importantes de las ciencias de la computación y su principal objetivo es establecer los principios, técnicas y algoritmos para la generación y manipulación de imágenes mediante una computadora.