prueba
Unidad 4
miércoles, 30 de octubre de 2019
Relleno de polígonos
En geometría, un polígono es una figura plana compuesta por una secuencia finita de segmentos rectos consecutivos que cierran una región en el plano. Estos segmentos son llamados lados, y los puntos en que se intersecan se llaman vértices.
En un sentido amplio, se define como una región del espacio delimitada por un conjunto de líneas (aristas) y cuyo interior puede estar rellenado por un color o patrón dado.
La tarea de rellenar a figuras primitivas puede ser dividida en dos partes: la decisión de cuáles pixeles se tienen que rellenar (que depende de la forma de la primitiva modificada por el recortado), y la decisión más sencilla de cuál valor rellenarlos.
MÉTODO DE RELLENO DE POLÍGONOS CON COLOR
SCAN-LINE
Fila a fila van trazando lineas de color entre aristas. para scan-line que cruce el polígono se busca en la intersección entre las lineas de barrido y las aristas del polígono.
LINEA DE BARRIDO
Es valido para polígonos cóncavos como convexos. Incluso para si el objeto tiene huecos interiores.
Funcionan en el trozo de lineas horizontales, denominadas lineas de barridos, que intersectan un numero de veces, permitiendo a partir de ella identificar los puntos que se consideran interiores al polígono.
INUNDACIÓN
- Empieza en un interior y pinta hasta encontrar la frontera del objeto.
- Partimos de un punto inicial (x,y), un colo de relleno y un color de frontera.
- El algoritmo va testeando los píxeles vecinos a los ya pintados, viendo si son frontera o no.
- No solo sirven para polígonos, sino para cualquier área curva para cualquier imagen AE se usan los programas de dibujo.
FUERZA BRUTA
- Calcula una caja contenedora del objeto.
- Hace un barrido interno de la caja para comprobar c/pixel este dentro del polígono.
- Con polígonos simétricos basta con que hagamos un solo barrido en una sección y replicar los demás pixeles.
- Requiere aritmética punto-flotante, esto lo hace preciso y costoso.
ALTERNATIVAS PARA LA SITUACIÓN INICIAL DEL PATRÓN
Consiste en situar el punto asociado a la esquina superior izquierda del patrón en un vértice del polígono.
- Considerar la región a rellenar en toda la pantalla y por lo tanto el patrón se citua en el origen de esta (esquina superior izquierda).
EJEMPLO DE SCAN-LINE
- Encontrar las intersecciones de los scanlines en el polígono.
- Almacenar las intersecciones en alguna estructura de datos ET (edge table), de manera ordena ascendiente en Y y en X en buckets.
- Rellenar los spans usando la estructura.
- Usar algún criterio de paridad para saber cuando un intervalo debe ser rellenado o no.
Proyecto Factal
Un fractal es un objeto geométrico cuya estructura básica, fragmentada o aparentemente irregular, se repite a diferentes escalas.1 El término fue propuesto por el matemático Benoît Mandelbrot en 1975 y deriva del latín fractus, que significa quebrado o fracturado. Muchas estructuras naturales son de tipo fractal. La propiedad matemática clave de un objeto genuinamente fractal es que su dimensión métrica fractal es un número racional no entero.
Si bien el término "fractal" es reciente, los objetos hoy denominados fractales eran bien conocidos en matemáticas desde principios del siglo XX. Las maneras más comunes de determinar lo que hoy denominamos dimensión fractal fueron establecidas a principios del siglo XX en el ámbito de la teoría de la medida..
Si bien el término "fractal" es reciente, los objetos hoy denominados fractales eran bien conocidos en matemáticas desde principios del siglo XX. Las maneras más comunes de determinar lo que hoy denominamos dimensión fractal fueron establecidas a principios del siglo XX en el ámbito de la teoría de la medida..
lunes, 28 de octubre de 2019
jueves, 24 de octubre de 2019
Formas Geométricas Tridimensionales (Superficies planas y Curvas)
En este caso trataremos con las proyecciones que van del espacio al plano (3D a 2D). La proyección de objetos tridimensionales serán definidos por la intersección de líneas rectas que van desde un centro de proyección u ojo, hasta cada punto del objeto.
Proyección Acotada
Es una proyección ortogonal sobre la que se acotan en cada punto, línea, u objeto representado la altura (cota) del mismo con respecto a cualquier plano de referencia que sea paralelo al plano de proyección. La proyección acotada es muy práctica cuando es necesario representar gráficamente objetos irregulares; razón por la cual se usa frecuentemente para el diseño de techos de viviendas; construcción de puentes, represas, acueductos, gasoductos, carreteras, determinación de áreas de parcelas, trazado de linderos, y dibujos topográficos de plantas y perfiles de terrenos, entre otros.
Proyección Cónica.
Denominada también perspectiva. Se obtiene cuando el punto de observación y el objeto se encuentran relativamente cercanos. Es el sistema de representación gráfico en donde el haz de rayos proyectantes confluye en un punto (el ojo del observador), proyectándose la imagen en un plano auxiliar situado entre el objeto a representar y el punto de vista.

PROYECCIÓN ORTOGONAL
La Proyección ortogonal es aquella cuyas rectas proyectantes auxiliares son perpendiculares al plano de proyección (o a la recta de proyección), estableciéndose una relación entre todos los puntos del elemento proyectante con los proyectados.
Existen diferentes tipos:
Vista A: Vista frontal o alzado
Vista B: Vista superior o planta
Vista C: Vista derecha o lateral derecha
Vista D: Vista izquierda o lateral izquierda
Vista E: Vista inferior
Vista F: Vista posterior

PROYECCIÓN OBLICUA.
Es aquella cuyas rectas proyectantes auxiliares son oblicuas al plano de proyección, estableciéndose una relación entre todos los puntos del elemento proyectante con los proyectados.
Una proyección Oblicua se obtiene proyectando puntos a lo largo de líneas paralelas que no son perpendiculares al plano de proyección. La figura muestra una proyección oblicua de un punto (x, y, z) por una línea de proyección a la posición (xp, Yp).

ECUACIONES DE PLANO
Los parámetros que especifican la orientación especial de cada polígono se obtienen de los valores coordenados de los vértices y las ecuaciones que definen los planos poligonales. Estos parámetros de planos se utilizan en transformaciones de visión, modelos de sombreado y algoritmos de superficies ocultas que determinan que líneas y planos se traslapan a lo largo de la línea de visión.
La ecuación de una superficie plana puede expresarse así: Ax + By + Cz + D = 0
Donde (x,y,z) es cualquier punto de plano. Los coeficientes A, B, C, D son constantes que pueden calcularse utilizando los valores coordenados de tres puntos no coloniales en el plano. Comúnmente, se usan las coordenadas de tres vértices sucesivos en una frontera de un polígono para hallar valores de estos coeficientes. Al denotar las coordenadas de tres vértices de un polígono como (x1, y1, z1), (x2, y2, z2) y (x3, y3, z3), se puede resolver el siguiente conjunto de ecuaciones planas simultáneas para las razones A/D, B/D y C/D:
(A / D)xi + (B / D)yi + (C / D)zi = -1 i = 1, 2, 3
Utilizando un método de solución como la regla de Cramer, se puede escribir la solución de los parámetros del plano en forma de determinantes:
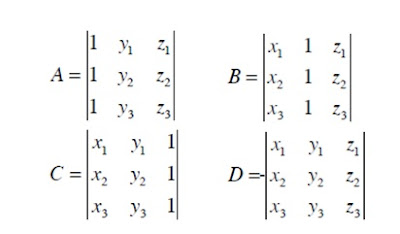
Podemos ampliar los determinantes y escribir los cálculos de los coeficientes del plano en la forma explícita:
A = y1(z2 − z3 ) + y2 (z3 − z1) + y3(z1 − z2 )
B = z1(x2 − x3 ) + z2 (x3 − x1) + z3(x1 − x2 )
C = x1(y2 − y3 ) + x2 (y3 − y1) + x3(y1 − y2 )
D = −x1(y2z3 − y3z2 ) − x2 (y3z1 − y1z3 ) − x3(y1z2 − y2z1)
Los valores de A, B, C y D se almacenan en la estructura de datos que contiene la información de coordenadas y atributos referente al polígono definido en este plano.
La orientación de una superficie plana se especifica por medio del vector normal al plano, como se muestra en la figura 1.4.Este vector normal tridimensional tiene las coordenadas cartesianas (A, B, C).
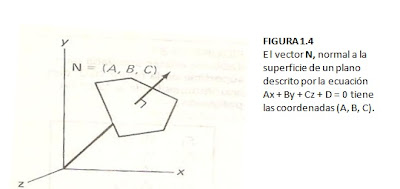
Puesto que con frecuencia trabajamos con superficies poligonales que encierran un objeto interior, se necesita distinguir entre los lados de la superficie.
El lado del plano que da la cara al objeto interior se denomina “interior” y el lado visible o externo se llama “exterior”. Si se especifican vértices en un sentido igual al del reloj cuando se observa el lado externo del plano en su sistema coordenado por la derecha, la dirección del vector normal ira de adentro hacia afuera. Esto se demuestra para un plano de un cubo unitario de la figura 1.5.
Para determinar los componentes del vector normal de la superficie sombreada que se muestra en la figura 1.5, se seleccionan tres de los cuatros vértices situados a lo largo de la frontera del polígono.
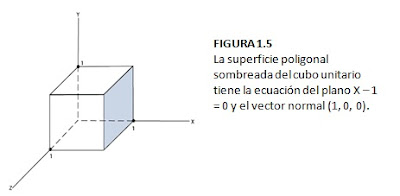
Estos puntos se seleccionan en un sentido igual al del reloj cuando observamos el exterior del cubo hacia el origen.
Las coordenadas de estos vértices, en el orden seleccionado, se utilizan en la ecuacion de la figura 1.4 a fin de obtener los coeficientes del plano:
A = 1, B = 0, C = 0, D = -1. El vector normal de este plano esta en el sentido del eje x positivo.Las ecuaciones del plano se utiliza también para identificar puntos interiores y exteriores. Cualquier punto (x, y, z) exterior aun plano satisface la desigualdad.
Ax + By + Cz + D > 0
Análogamente, cualquier punto situado en el interior del plano produce un valor negativo de la expresión Ax + By + Cz + D. Para la superficie sombreada de la figura 1.5, cualquier punto exterior al plano cumple la desigualdad x - 1 < 0, mientras que cualquier punto interior al plano tiene un valor de coordenadas x menor que 1.
SUPERFICIES CURVAS
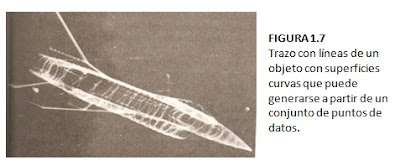
Los despliegues tridimensionales de las superficies curvas pueden generarse a partir de un conjunto de entrada de las funciones matemáticas que define las superficies o bien a partir de un conjunto de puntos de datos especificados por el usuario. Cuando se especifican funciones de curvas, un paquete puede emplear las ecuaciones definidoras para localizar y graficar posiciones de pixeles a lo largo de la trayectoria de la curva, casi igual como sucede con las curvas en dos dimensiones. Un ejemplo de la clase de superficies que pueden generarse a partir de una definición funcional se da en la figura 1.6. A partir de un conjunto de datos de entrada, un paquete determina las descripciones funcionales de la curva que mejor se ajusta a los puntos de datos según las restricciones de la aplicación. En la figura 1.7 se muestra un objeto cuyas superficies curvas pueden ser definidas por un conjunto de entrada de punto de datos.
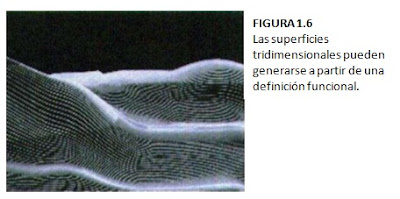
Podemos representar una línea curva tridimensional en forma analítica con la pareja de funciones.
y=f(x), z=g(x)
Con la coordenada x seleccionada como variable independiente. Los valores de las variables dependientes y, z se determinan después a partir de las ecuaciones 1.6 a medida que se avanza a través de valores de x de un extremo de la línea al otro. Esta representación tiene algunas desventajas. Si se desea una grafica alisada, se debe cambiar la variable independiente siempre que la primera derivada (pendiente) de f(x) o bien g(x) se vuelve mayor que 1. Esto significa que se debe verificar continuamente los valores de las derivadas, que pueden volverse infinitas en algunos puntos. Asimismo, las ecuaciones anteriores ofrecen un formato desproporcionado para representar funciones con valores múltiples. Una representación más propicia de las curvas para aplicaciones de las graficas es en términos de ecuaciones paramétricas.
Formas Geométricas
Representación y Visualización de Objetos en Tres Dimensiones.
El diseño ayudado por ordenador representa un gran ahorro de esfuerzo y tiempo. Además se consiguen resultados extraordinarios con respecto a los procedimientos clásicos de diseño. Los programas de diseño industrial o arquitectónico admiten tres maneras de representación de objetos.
Modelos bidimensionales del objeto o parte de él. Se reproducen separadamente las diferentes caras, planos o cortes para ser estudiados y modificados. Normalmente se utiliza una representación formal del objeto, obteniendo sus vistas desde diferentes puntos de visualización. Se denominan vistas principales de un objeto, a las proyecciones ortogonales del mismo sobre 6 planos, dispuestos en forma de cubo. También se podría definir las vistas como, las proyecciones ortogonales de un objeto, según las distintas direcciones desde donde se mire. Si situamos un observador según las seis direcciones indicadas por las flechas, obtendríamos las seis vistas posibles de un objeto.
Modelos tridimensionales que incluyan únicamente un conjunto de puntos y líneas en el espacio. Estos modelos se llaman “wireframe” o alambrado (armazón de alambre). El objeto así representado rota en diferentes ángulos para su estudio o transformación definitiva. Existen varias formas de representación en modo wireframe:
1. Representación alambrica: Activa este modo de sombreado.
2. Representación alambrica det: Se muestran bordes alámbricos e iluminación
3. Área de trabajo: Muestra los objetos como área de trabajo solamente. El área de trabajo se define como la caja más pequeña que abarca completamente un objeto.
Formas geométricas espaciales
Figura
Imagen
Pirámide

Prisma

Cilindro

Cono

Esfera
Elipsoide

Paraboloide

Hiperboloide
 |
Espacio tridimensional
El espacio 3D es un espacio matemático virtual creado por el programa de diseño 3D. Este espacio está definido por un sistema cartesiano de tres ejes: X, Y, Z. El punto donde salen las líneas virtuales que definen los ejes se llama origen y sus coordenadas son (0, 0, 0). En este espacio virtual se crean, modifican y disponen los diferentes objetos tridimensionales que van a componer la escena.
Renderizado
El renderizado es un proceso de cálculo complejo desarrollado por un ordenador destinado a generar una imagen 2D a partir de una escena 3D. Así podría decirse que en el proceso de renderización, la computadora "interpreta" la escena 3D y la plasma en una imagen 2D.
La renderización se aplica a los gráficos por ordenador, más comúnmente a la infografía. En infografía este proceso se desarrolla con el fin de imitar un espacio 3D formado por estructuras poligonales, comportamiento de luces, texturas, materiales, animación, simulando ambientes y estructuras físicas verosímiles, etc. Una de la partes más importantes de los programas dedicados a la infografía son los motores de render los cuales son capaces de realizar técnicas complejas como radiosidad, raytrace (trazador de rayos), canal alpha, reflexión, refracción, iluminación global, etc.
Cuando se trabaja en un programa de diseño 3D por computadora, no es
posible visualizar en tiempo real el acabado final deseado de una escena 3D compleja ya que esto requiere una potencia de cálculo demasiado elevada. Por lo que se opta por crear el entorno 3D con una forma de visualización más simple y técnica y luego generar el lento proceso de renderización para conseguir los esultados finales deseados.
Proyecciones
En dos dimensiones, las operaciones de visión transfieren puntos bidimensionales en el plano coordenado mundial a puntos bidimensionales en el plano de coordenadas del dispositivo. Las definiciones de objetos, sujetados contra el marco de una ventana, se delinean en un puerto de visión (viewport). Estas coordenadas de dispositivo normalizadas se convierten después en coordenadas de dispositivo y el objeto se despliega en el dispositivo de salida.
En tres dimensiones, la situación es un poco más complicada, ya que ahora tenemos algunas alternativas como la forma en que se van a generar las vistas. Podríamos visualizar una escena desde el frente, desde arriba o bien desde atrás. También podríamos generar una vista de lo que observaríamos si estuviéramos parados en medio de un grupo de objetos. Además, las descripciones tridimensionales de objetos deben proyectarse en la superficie de visión plana del dispositivo de salida.
La visualización en nuestro caso significa información del mundo real en la pantalla. La visualización 2D son las operaciones de transferencia de puntos bidimensionales en el plano coordenado del mundo en el plano coordenado del dispositivo.
Existen dos métodos básicos para proyectar objetos tridimensionales sobre una superficie de visión bidimensional. Estas dos maneras, dependen de si todos los puntos del objeto pueden proyectarse sobre la superficie a lo largo de líneas paralelas o bien los puntos pueden proyectarse a lo largo de líneas que convergen a una posición denominada centro de proyección. En ambos casos, la intersección de una línea de proyección con la superficie de visión determina las coordenadas del punto proyectado sobre este plano de proyección.
lunes, 14 de octubre de 2019
Curvas
Curvas de B-Spline
En el subcampo matemático de análisis numérico, una B-spline o Basis spline (o traducido una línea polinómica suave básica), es una función spline que tiene el mínimo soporte con respecto a un determinado grado, suavidad y partición del dominio. Un teorema fundamental establece que cada función spline de un determinado grado, suavidad y partición del dominio, se puede representar como una combinación lineal de B-splines del mismo grado y suavidad, y sobre la misma partición. El término B-spline fue acuñado por Isaac Jacob Schoenberg y es la abreviatura de spline básica. Las B-splines pueden ser evaluadas de una manera numéricamente estable por el algoritmo de Boor. De un modo simplificado, se han creado variantes potencialmente más rápidas que el algoritmo de Boor, pero adolecen comparativamente de una menor estabilidad.
En el subcampo de la informática de diseño asistido por computadora y de gráficos por computadora, el término B-spline se refiere con frecuencia a una curva parametrizada por otras funciones spline, que se expresan como combinaciones lineales de B-splines (en el sentido matemático anterior). Una B-spline es simplemente una generalización de una curva de Bézier, que puede evitar el fenómeno Runge sin necesidad de aumentar el grado de la B-spline

Curvas Fractales
Las curvas fractales son dibujos que se definen repitiéndose a si mismos a diferentes niveles. Un ejemplo típico es la Curva de Hilbert. A continuación mostramos la construcción de una curva de Hilbert de orden 3 (o nivel 3) usando el lenguaje de programación Logo:

Estas curvas pueden ser dibujadas usando procedimiento recursivos, es decir procedimientos que se llaman a si mismos. La curva de Hilbert de orden 1 es la más sencilla y constituye el caso base. Podría definirse así:
para hilbert_1 | 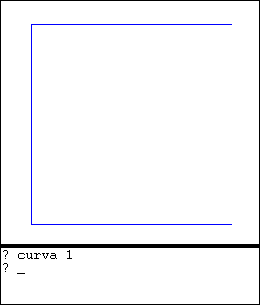 |
Usando la curva de orden 1 como base, podemos definir la curva de orden 2, así:
para hilbert_2 | 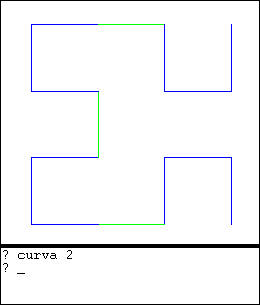 |
Ya que ambos procedimientos tienen la misma estructura puede definirse un procedimiento general:
para hilbert :nivel :angulo
si :nivel < 1 [alto]
giraizquierda :angulo
hilbert :nivel - 1 (cambiasigno :angulo)
segmento
giraderecha :angulo
hilbert :nivel - 1 :angulo
segmento
hilbert :nivel - 1 :angulo
giraderecha :angulo
segmento
hilbert :nivel - 1 (cambiasigno :angulo)
giraizquierda :angulo
fin
para segmento
poncolorlapiz :nivel
avanza :tam
fin
Para centrar la curva fractal en la pantalla y para definir correctamente la longitud de cada segmento usamos el procedimiento curva:
para curva :nivel
haz "tam 200 / (-1 + potencia 2 :nivel)
borrapantalla
subelapiz ponpos [100 -70] bajalapiz
hilbert :nivel 90
fin
Los estructuras fractales en general tienen la propiedad de auto-similitud. Es decir que, si observamos una parte de la estructura como con un microscopio lo que observamos es similar, a lo que observamos a simple vista.
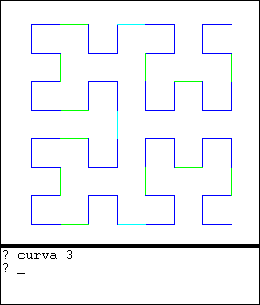 | 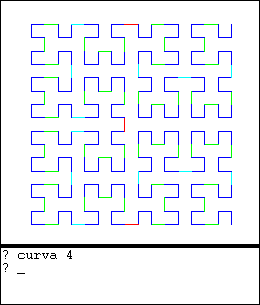 |
 |  |
La curva fractal de Hilbert tiene la curiosa propiedad de que cuando el orden de la curva tiende al infinito, la curva tiende a cubrir el espacio. Es decir, el límite de esta curva unidimensional cubre un espacio bi-dimensional cuadrado.
 | 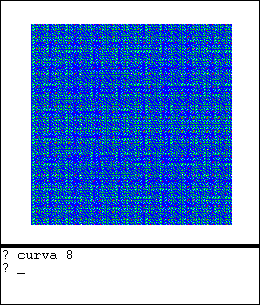 |
Suscribirse a:
Comentarios (Atom)
Unidad 5: Introducción a la animación por computadora
Introducción a la animación por computadora 5.1 Historia, evolución y aplicación de la graficación por computadora. 1919-1990 Cr...
-
Traslación Una traslación es el movimiento en línea recta de un objeto de una posición a otra. Movimiento de una figura, sin rota...
-
En este caso trataremos con las proyecciones que van del espacio al plano (3D a 2D). La proyección de objetos tridimensionales serán definid...