Curvas

Curvas de B-Spline

En el subcampo matemático de análisis numérico, una B-spline o Basis spline (o traducido una línea polinómica suave básica), es una función spline que tiene el mínimo soporte con respecto a un determinado grado, suavidad y partición del dominio. Un teorema fundamental establece que cada función spline de un determinado grado, suavidad y partición del dominio, se puede representar como una combinación lineal de B-splines del mismo grado y suavidad, y sobre la misma partición.​ El término B-spline fue acuñado por Isaac Jacob Schoenberg y es la abreviatura de spline básica. Las B-splines pueden ser evaluadas de una manera numéricamente estable por el algoritmo de Boor. De un modo simplificado, se han creado variantes potencialmente más rápidas que el algoritmo de Boor, pero adolecen comparativamente de una menor estabilidad.

En el subcampo de la informática de diseño asistido por computadora y de gráficos por computadora, el término B-spline se refiere con frecuencia a una curva parametrizada por otras funciones spline, que se expresan como combinaciones lineales de B-splines (en el sentido matemático anterior). Una B-spline es simplemente una generalización de una curva de Bézier, que puede evitar el fenómeno Runge sin necesidad de aumentar el grado de la B-spline

Curvas Fractales

Curvas fractales o recursivas, usando el lenguaje de programación Logo (Intérprete FMSLogo).

Las curvas fractales son dibujos que se definen repitiéndose a si mismos a diferentes niveles. Un ejemplo típico es la Curva de Hilbert. A continuación mostramos la construcción de una curva de Hilbert de orden 3 (o nivel 3) usando el lenguaje de programación Logo:

Estas curvas pueden ser dibujadas usando procedimiento recursivos, es decir procedimientos que se llaman a si mismos. La curva de Hilbert de orden 1 es la más sencilla y constituye el caso base. Podría definirse así:

para hilbert_1 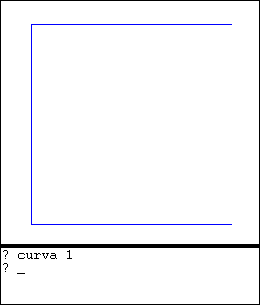giraizquierda 90 segmento giraderecha 90 segmento giraderecha 90 segmento giraizquierda 90 fin para segmento avanza 200 fin

Usando la curva de orden 1 como base, podemos definir la curva de orden 2, así:

para hilbert_2 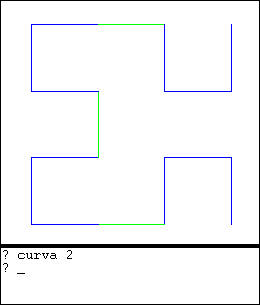giraizquierda 90 hilbert_1 -90 segmento giraderecha 90 hilbert_1 90 segmento hilbert_1 90 giraderecha 90 segmento hilbert_1 -90 giraizquierda 90 fin para hilbert_1 :ang giraizquierda :ang segmento giraderecha :ang segmento giraderecha :ang segmento giraizquierda :ang fin para segmento avanza 200 / (4 - 1) fin

Ya que ambos procedimientos tienen la misma estructura puede definirse un procedimiento general:

para hilbert :nivel :angulo
si :nivel < 1 [alto]

giraizquierda :angulo
hilbert :nivel - 1 (cambiasigno :angulo)
segmento
giraderecha :angulo
hilbert :nivel - 1 :angulo
segmento
hilbert :nivel - 1 :angulo
giraderecha :angulo
segmento
hilbert :nivel - 1 (cambiasigno :angulo)
giraizquierda :angulo
fin

para segmento
poncolorlapiz :nivel
avanza :tam
fin

Para centrar la curva fractal en la pantalla y para definir correctamente la longitud de cada segmento usamos el procedimiento curva:

para curva :nivel
haz "tam 200 / (-1 + potencia 2 :nivel)

borrapantalla
subelapiz ponpos [100 -70] bajalapiz

hilbert :nivel 90
fin

Los estructuras fractales en general tienen la propiedad de auto-similitud. Es decir que, si observamos una parte de la estructura como con un microscopio lo que observamos es similar, a lo que observamos a simple vista.

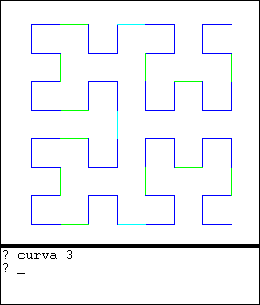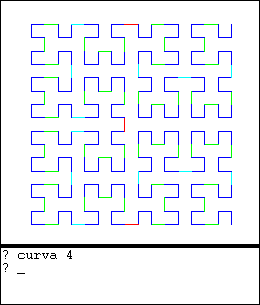La curva fractal de Hilbert tiene la curiosa propiedad de que cuando el orden de la curva tiende al infinito, la curva tiende a cubrir el espacio. Es decir, el límite de esta curva unidimensional cubre un espacio bi-dimensional cuadrado.