Historia
Forma elíptica trazada en la antigüedad
sobre un muro de Tebas (Egipto)
La elipse, como curva geométrica, fue
estudiada por Menecmo, investigada por Euclides, y su nombre se atribuye a
Apolonio de Pérgamo. El foco y la directriz de la sección cónica de una elipse
fueron estudiadas por Pappus. En 1602, Kepler creía que la órbita de Marte era
ovalada, aunque más tarde descubrió que se trataba de una elipse con el Sol en
un foco. De hecho, Kepler introdujo la palabra «focus» y publicó su descubrimiento
en 1609. Halley, en 1705, demostró que el cometa que ahora lleva su nombre
trazaba una órbita elíptica alrededor del Sol.4
Elementos de una elipse
La elipse y algunas de sus propiedades
geométricas
La elipse es una curva plana y cerrada,
simétrica respecto a dos ejes perpendiculares entre sí:
Puntos de una elipse
Los focos de la elipse son dos puntos
equidistantes del centro, F1 y F2 en el eje mayor. La suma de las distancias
desde cualquier punto P de la elipse a los dos focos es constante, e igual a la
longitud del diámetro mayor (d(P,F1)+d(P,F2)=2a).
Por comodidad denotaremos por PQ la
distancia entre dos puntos P y Q.
Si F1 y F2 son dos puntos de un plano, y 2a
es una constante mayor que la distancia F1F2, un punto P pertenecerá a la
elipse si se cumple la relación:
Ejes de una elipse
El eje mayor, 2a, es la mayor distancia
entre dos puntos opuestos de la elipse. El resultado de la suma de las
distancias de cualquier punto a los focos es constante y equivale al eje mayor.
El eje menor 2b, es la menor distancia entre dos puntos opuestos de la elipse.
Los ejes de la elipse son perpendiculares entre sí.
Excentricidad de una elipse
La excentricidad ε (épsilon) de una elipse
es la razón entre su semidistancia focal (longitud del segmento que parte del
centro de la elipse y acaba en uno de sus focos), denominada por la letra c, y
su semieje mayor. Su valor se encuentra entre cero y uno.
La excentricidad indica la forma de una
elipse; una elipse será más redondeada cuanto más se aproxime su excentricidad
al valor cero.5La designación tradicional de la excentricidad es la letra
griega ε llamada épsilon.
(No se debe usar la letra e para
designarla, porque se reserva para la base de los logaritmos naturales o
neperianos. Véase: número e).
Excentricidad angular de una elipse
La excentricidad angular, esto es:
Constante de la elipse
En la figura de la derecha se muestran los
dos radio vectores correspondientes a cada punto P de una elipse, los vectores
que van de los focos F1 y F2 a P. Las longitudes de los segmentos
correspondientes a cada uno son PF1 (color azul) y PF2 (color rojo), y en la
animación se ilustra como varían para diversos puntos P de la elipse.
Como establece la definición inicial de la
elipse como lugar geométrico, para todos los puntos P de la elipse la suma de
las longitudes de sus dos radio vectores es una cantidad constante igual a la
longitud 2a del eje mayor:
PF1 + PF2 = 2a
En la elipse de la imagen 2a vale 10 y se
ilustra, para un conjunto selecto de puntos, cómo se cumple la definición.
Concepto y elementos de la elipse
Es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante.


Elementos de la elipse:
1. Focos: Son los puntos fijos F y F'.
2. Eje focal: Es la recta que pasa por los focos.
3. Eje secundario: Es la mediatriz del segmento FF'.
4. Centro: Es el punto de intersección de los ejes.
5. Radios vectores: Son los segmentos que van desde un punto de la elipse a los focos: PF y PF'.
6. Distancia focal: Es el segmento segmento de longitud 2c, c es el valor de la semidistancia focal.
7. Vértices: Son los puntos de intersección de la elipse con los ejes: A, A', B y B'.
8. Eje mayor: Es el segmento segmento de longitud 2a, a es el valor del semieje mayor.
9. Eje menor: Es el segmento segmento de longitud 2b, b es el valor del semieje menor.
10. Ejes de simetría: Son las rectas que contienen al eje mayor o al eje menor.
11. Centro de simetría: Coincide con el centro de la elipse, que es el punto de intersección de los ejes de simetría.
Relación entre la distancia focal y los semiejes



Elementos de la elipse:
1. Focos: Son los puntos fijos F y F'.
2. Eje focal: Es la recta que pasa por los focos.
3. Eje secundario: Es la mediatriz del segmento FF'.
4. Centro: Es el punto de intersección de los ejes.
5. Radios vectores: Son los segmentos que van desde un punto de la elipse a los focos: PF y PF'.
6. Distancia focal: Es el segmento segmento de longitud 2c, c es el valor de la semidistancia focal.
7. Vértices: Son los puntos de intersección de la elipse con los ejes: A, A', B y B'.
8. Eje mayor: Es el segmento segmento de longitud 2a, a es el valor del semieje mayor.
9. Eje menor: Es el segmento segmento de longitud 2b, b es el valor del semieje menor.
10. Ejes de simetría: Son las rectas que contienen al eje mayor o al eje menor.
11. Centro de simetría: Coincide con el centro de la elipse, que es el punto de intersección de los ejes de simetría.
Relación entre la distancia focal y los semiejes

A continuación se presenta unos ejercicios resolvimos en clases y graficamos en geogebra :
resolvimos también en geogebra:
ejercicio 2
graficamos en GeoGebra:
ejercicio 3:
ejercicios 4:




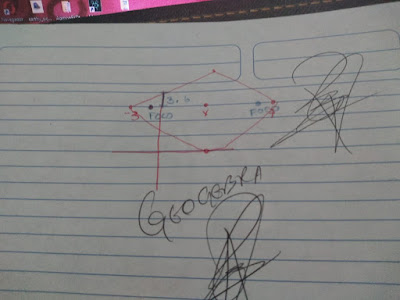






...viaje interestelar aceleración constante (órbitas elípticas, katherine johnson)... e, excentricidad >0 y <1 su grado de alargamiento; e= cos B/cos a... elípse, si se define como curva cerrada de la intersección de un plano que corta a una superficie cónica sin pasar por su vértice; a, ángulo de la superficie cónica entre su eje y generatriz; B, ángulo >a y <90º entre el plano y el eje de la superficie cónica.
ResponderBorrar...frenando asteroides, el método más expeditivo: colocar "las nucleares" muy cerca de la superficie... "Boom!", en el Espacio, al no haber aire no hay onda expansiva, lo único que le llega es la radiación que volatiliza el material del punto de impacto y produciendo un chorro a reacción que cambia su órbita... (pag. 135-138. Libro "El Asteroide del Fin del Mundo")
ResponderBorrarEste comentario ha sido eliminado por el autor.
ResponderBorrarEste comentario ha sido eliminado por el autor.
ResponderBorrarEste comentario ha sido eliminado por el autor.
BorrarEste comentario ha sido eliminado por el autor.
ResponderBorrarEste comentario ha sido eliminado por el autor.
ResponderBorrarEste comentario ha sido eliminado por el autor.
Borrar...viaje interestelar constante aceleración (hipótesis tonyon)... "la velocidad orbital de los electrones varía inversamente a la aceleración", gravitatoria o de movimiento. Por eso en Marte con menor aceleración gravitatoria un reloj atómico va más rápido que en la Tierra. Es el reloj el que atrasa o adelanta, no "el Tiempo".
ResponderBorrar(3a)...viaje interestelar constante aceleración (hipótesis tonyon)... con los futuros Transformadores Gravitatorios: qué pasaría si... Nave Estelar a 1 Millón G... Áreas habitables: 1M-g de aceleración constante hacia el suelo ↓↓motores↓↓ (-) 999 999g de aceleración constante hacia el techo ↑↑transformadores gravitatorios↑ = 1g de aceleración constante hacia el suelo↓... Áreas habitables: 2 relojes atómicos fuera y 2 dentro. Los 2 dentro funcionan a 1g normalmente. Los 2 de fuera a 1M-g... quizás sus electrones se quedarían parados en sus órbitas: Los 2 relojes de fuera se pararían, no "el Tiempo" de fuera sí y el de dentro no. Si la atracción electromagnética protón/electrón fuera más fuerte que las fuerzas de la enorme aceleración sobre los electrones, los electrones caerían al núcleo atómico quedando los átomos con sus electrones parados pegados al núcleo... Sin electrones de valencia ya no hay moléculas... Qué pasaría con la estrucrura de la Nave ("eso es la Materia, sobre todo espacio vacío") ya de Materia formada por átomos con los electrones parados en sus órbitas, o por átomos con sus electrones parados y pegados al núcleo: la estructura de la Nave se derrumbaría como arena sin cemento... Para evitar el "efecto aceleración" poner los Transformadores Gravitatorios en TODA la estructura de la Nave, no solo en las áreas habitables. Así la Nave entera siente 1g aunque vaya a 1M-g, (1Mega-g).
Borrar...viaje interestelar constante aceleración (tonyon - Antonio Iglesias Noja - proyecto GSENA: Global Solar Energy No Accumulation)... del S☼L→ a la S☺mbra del giratorio Planeta envío recíproco Global de Electricidad por Cables Submarinos... Cubrir Desiertos con Paneles Solares en alto (bajo ellos el suelo mejora)... Sin "esos" malditos patriotas contra el Progreso de la Humanidad cortando los Cables.
ResponderBorrarEste comentario ha sido eliminado por el autor.
ResponderBorrar(El Imán Más Fuerte del Mundo. Veritasium. YouTube). Levitación por la Ley de Lenz: corrientes inducidas en materiales no magnéticos sí conductores como Al, Cu. Todos los materiales tienen propiedades magnéticas: el agua es diamagnética: levitación de frutas y seres vivos.
ResponderBorrar